Encuesta de Bachiller IPANU

MEDIDAS DE DISPERSIÓN

Las medidas de dispersión es el cálculo del rango, desviación estándar .

-Rango:

       Se obtiene a partir de restar el límite superior menos el límite inferior.

-Desviación estándar:

       Antes de realizarla, se debe obtener la media, restar cada uno de los datos y al resultado sacar la raíz cuadrada. Sumamos todos los resultados y la cantidad obtenida la dividimos entre el total de datos.

-Variabilidad:

       De la cantidad obtenida de la desviación estándar se saca el cuadrado y ese será el resultado.

MEDIDAS DE TENDENCIA CENTRAL

Las medidas de tendencia central es el cálculo de la media, mediana y moda.

-Media:

       Se obtiene a partir de la suma de todos los datos divididos entre la cantidad de los mismos.

-Moda:

       En el número que se repite más veces.

-Mediana:

       Una vez acomodados los valores de menor a mayor se toma el valor que está justo en medio.

TIPOS DE GRÁFICAS

• Variable Cualitativa:

*Gráfica de barras:

Es un método gráfico que consta de dos ejes: Uno horizontal, en el que se representan los valores (Eje de los datos) utilizando barras verticales en forma rectangular y de la misma amplitud, y un eje vertical, en el cual la frecuencia representa la altitud que tendrá la barra rectangular (Eje de las frecuencias), las barras van separadas la misma distancia unas de otras y para distinguirlas puede utilizarse distintos colores o entramados según se considere. 

*Gráfica de Pastel o circular:

Este gráfico se utiliza fundamentalmente, para representar distribuciones de frecuencias relativas (es decir, porcentajes % o proporciones) haciendo corresponder la medida de la frecuencia relativa con la medida del ángulo en grados; es decir, si el 100 % de los datos son 360º de la circunferencia, a cada 1% le corresponderán 3.6º; así, para obtener la medida del ángulo del sector, multiplicamos la frecuencia correspondiente por 3.6º. Al utilizar este gráfico se aconseja no sobrepasar los 10 elementos, y ordenar los sectores de acuerdo a una de dos formas, ya sea siguiendo el orden que se les dé a los datos o empezando del mayor al menor segmento, iniciando a partir de las 12 horas y en el sentido de las manecillas del reloj. Por último, si el texto que representa cada sector no puede colocarse dentro del mismo, se elabora una leyenda que se coloca fuera del segmento, unidos por una flecha.  

                    

*Gráfica de columnas

muestra una serie como un conjunto de barras verticales agrupadas por categorías. Los gráficos de columnas resultan de gran utilidad para mostrar los cambios que se producen en los datos a lo largo del tiempo o para ilustrar comparaciones entre elementos. El gráfico de columnas sencillo está estrechamente relacionado con el gráfico de barras, que muestra las series como conjuntos de barras horizontales, y con el gráfico de intervalos de columnas, que muestra las series como conjuntos de barras verticales con puntos iniciales y finales que varían.

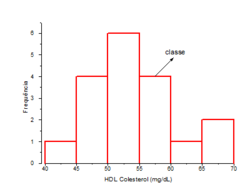
*Histograma:

Esta representación gráfica se utiliza cuando la variable toma valores sobre una escala de intervalo o de razón. En el eje horizontal se ubican los valores de la variable representados por medio de sus marcas de clase, y en el eje vertical se localizan las frecuencias de cada intervalo. De esta manera, el histograma se compone de una serie de rectángulos, cada uno de los cuales tiene como base un intervalo de clase y la frecuencia como altura.

*Polígono de frecuencias

Es una representación gráfica que contempla la misma información que el histograma; en el eje horizontal se colocan los datos de la variable representados por las marcas de clase de cada intervalo, y en el eje vertical las frecuencias , ya sean absolutas o relativas. La diferencia radica en que en lugar de dibujar los rectángulos, se unen con una línea los puntos donde se interceptan las marcas de clase y las frecuencias de cada intervalo.

*Polígono de frecuencias acumuladas

Es una representación gráfica que contempla la misma información que el histograma; en el eje horizontal se colocan los datos de la variable representados por las marcas de clase de cada intervalo, y en el eje vertical las frecuencias , ya sean absolutas acumuladas y/o frecuencias relativas acumuladas. La diferencia radica en que en lugar de dibujar los rectángulos, se unen con una línea los puntos donde se interceptan las marcas de clase y las frecuencias de cada intervalo.

TIPOS DE DISTRIBUCIÓN DE FRECUENCIAS

• No agrupados:

Datos diferentes: Consideraremos como un dato diferente, a cada uno de los distintos datos que se presentan en la muestra, los denotaremos por i x , y al número total de datos diferentes lo denotaremos por m . 

Datos no Agrupados: Cuando el tamaño de la muestra (n) es finito y el número de datos diferentes es pequeño (consideraremos pequeño k ≤ 10), es fácil hacer un análisis de los datos tomando cada uno de los datos diferentes y ordenándolos.

• Agrupados:

Cuando el tamaño de la muestra es considerable o grande y los datos numéricos son muy diversos (n>15), conviene agrupar los datos de tal manera que permita establecer patrones, tendencias o regularidades.

BIENVENIDOS

Hola, mi nombre es Rosa Irene, estudiante de 5to semestre de Bachiller, este blog fue creado como actividad semestral y con el fin de proporcionar a todos los visitantes información sobre nuestras actividades realizadas en la materia de Probabilidad y Estadística I.

Espero que este Blog sea de su utilidad y agrado. 

CONCEPTOS BÁSICOS DE ESTADÍSTICA

Población:

Es el conjunto de elementos o unidades de interés. Son todos los objetos bajo discusión y acerca de los cuales se desea información. Una población puede tener un número finito o infinito de objetos.

Existen dos tipos de población: población objetivo, la cual hace referencia al conjunto de individuos sobre los cuales se hace inferencia y población muestreada, la cual constituye el marco muestral, es decir, aquellos individuos con posibilidad de ser seleccionados.

Muestreo:

Es la técnica para la selección de una muestra a partir de una población. Al elegir una muestra aleatoria se espera conseguir que sus propiedades sean extrapolables a la población. Este proceso permite ahorrar recursos, y a la vez obtener resultados parecidos a los que se alcanzarían si se realizase un estudio de toda la población.

Elemento:

Es cualquier elemento o ente que sea portador de información sobre alguna propiedad en la cual se está interesado.

Estudio:

Es toda acción o prueba que se realiza con el fin de observar su resultado.

Parámetro:

Son los valores o cantidades desconocidas que son obtenidas de, o que hacen referencia a las características de una población.

Estadística:

Es la rama de las matemáticas que se sirve de un conjunto de métodos, normas, reglas y principios para la observación, toma, organización, descripción, presentación y análisis del comportamiento de un grupo de datos para la conclusión sobre un experimento o fenómeno.